Conceptual Distance of Models and Languages

(based on [GR19a])

Conceptual distance (i.e., measurement of the distance between two sets of concepts) had its roots in linguistics as the semantic distance problem. In the linguistics context, conceptual distance provides a metric of the difficulty in understanding a topic across different disciplines or subject areas. However, it seems that there is no commonly agreed and well-founded theory that allows measurement of the distance between two sets of concepts. We believe that it is worthwhile to measure the conceptual distance between models, and also between languages.

In the domain of conceptual modeling, which emerged from entity–relationship modeling, models are usually explicit, describing the concepts (e.g., classes in OO), their properties (e.g., attributes in OO) and relationships (e.g., associations in OO). The conceptual distance between two models can be measured syntactically by comparing commonly occurring concepts, properties and relationships, versus elements that only exist in one of the models. This is easy to implement, but does not reflect that semantically equivalent models may exist, even if their syntactic representations differ. The syntactic differences may emerge from the use of synonyms for similar terms, or from structurally equivalent but unequal concept/relationship formalizations. A conceptual distance measurement based on semantic differences should consider the semantics of two conceptual models and compare the sets of described instances in a meaningful way. In conceptual modeling, semantics is usually an infinite set of instances (e.g., object structures in OO). Conceptual distance may be difficult to measure accurately.

In a development project, it is often desirable to identify differences of evolved versions of models. This is true for all modeling languages such as code, state machines, class diagrams, use case diagrams or any specific DSL. A pure syntactic interpretation of the conceptual distance can be defined generically by comparing the two models of a language and counting differences and similarities for each language construct (e.g., comparing “classes,” “attributes,” “states” or any other language construct). A somewhat smarter syntactic measurement could count “compatible” types as similar elements (e.g., int and long). Other similarity metrics could be based on the renaming of an element using a synonym. Such smart measurements exist and can assist in identifying variants of models in a product line development setting.

If the meaning of a model (i.e., its semantics) shall be used to measure conceptual distance of two models, then the situation becomes rather diverse. For the category of structural models (e.g., conceptual models, architectural models, block or class diagrams), conceptual distance of two models needs to compare the sets of possible instantiation structures (which are sets of sets of elements, e.g., objects). For the category of behavioral models, the set of possible behavior executions (e.g., sets of traces) and their differences should be analyzed. The conceptual distance of behavioral descriptions can be defined inductively over time, because there is a starting point, namely time point 0, from where all behaviors initiate. Similarity of behavior descriptions should typically regard the time point of the first deviation of two behavioral executions: The earlier the deviation can be observed, the larger the distance. All of these considerations are complicated by non-deterministic behavior of the described implementation, non-deterministic behavior of the environment, under specification of the models (which is not exactly the same, but similar to a non-deterministic implementation) and the possibility to add probabilities to all of the relevant concepts. This also contributes to the challenge of measuring conceptual distance accurately.

Beyond comparing individual model instances, it is also possible to compare the conceptual distance between two languages. Such a comparison can be helpful when there is a need to understand the differences between two programming languages, or also when trying to understand the differences between two modeling languages (or two variants of the same modeling language) that should be used for the same purpose. Two possibilities exist for such comparisons:

• (1) When using meta-models (or grammar) to describe languages, we can apply conceptual distance techniques to the meta-models (or grammars) similar to the instance models mentioned earlier
• (2) we can also analyze the distance by mapping one language construct to a similar construct in the other language (we will call this encoding)

This is very common when learning a new programming language by trying to understand how expressions, statements, case distinctions, loops, lambda abstractions or functions are defined in terms of other known languages. This mapping also assists in identifying the absence of a familiar and helpful construct in one language that may not be available in another language. However, this approach does not always allow objective measurements, but only give an informal understanding of the conceptual distance of languages. Using the encoding approach, we might argue that as the conceptual distance between languages increases, the complexity of the encoding also increases.

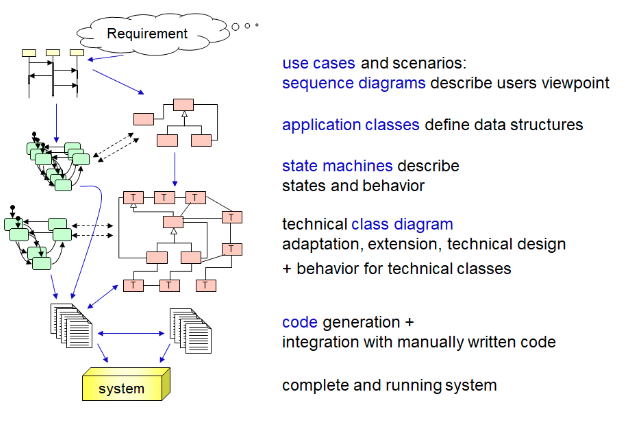
These observations lead us to an interesting point about software engineering, from the simple viewpoint of starting with a set of informal requirements, which are mapped down through several high-level and low-level model formalizations (as shown in the figure), and finally end up in an executable implementation. Between each of those modeling levels, the conceptual distance must be small enough such that we can manage a systematic, sound mapping between the levels. Usually, these mappings are not exactly systematic encodings, but also add a lot of additional human-constructed design decisions. However, the conceptual distance still needs to be kept manageable. As a natural consequence, in software-intensive complex systems we can observe with increasing frequency that the development paradigm used in the early stages may influence the implementation. For example, using a component connector architecture for high-level models of automotive software will probably lead to the explicit existence of components, connectors and ports in the final implementation. The explicit existence of these constructs that exist in the modeling languages creates overhead in the implementation, but also keeps the development process manageable, more efficient and potentially less erroneous. Furthermore, variant management and reusability will probably increase. A similar phenomenon occurs in workflow-intensive systems, where workflow descriptions are based on modeling techniques to organize and understand the system. Such systems vary explicitly know and manage the workflows and their respective states.

As a logical consequence, it can be observed that the form of the high-level modeling languages used to describe a system varies much according to the shapes, structure and architecture of the implementation, as well as the abstractions available in the implementation. This helps to keep the conceptual distance between requirements and implementation small and the development manageable. Interestingly, this is different from other engineering domains (e.g., architecture), where the existence or form of models and plans has no impact on the created building.

There is much more to be said about conceptual distance and it is in particular to be made more precise and thus measurable. We look forward to investigations into either comparisons of specific languages or as general considerations toward a theory of measuring conceptual distance.

This essay is essentially taken from a SoSyM editorial, which is published under the Creative Commons licence and contains some updates:

Further links:

• Essays, Comments, Definitions around Modeling
• Publications
• Topic sorted list of most interesting publications
• Books
• Website of the SE